Grundlagen digitaler Medientechnik
Grundlagen Audio (auch als pdf zum Offline-Lesen und Drucken)
Begriffe
Klang - Analyse
und Synthese
Digitalisierung
Datenübertragung und Speicherung
Aussteuerung
Interferenz / Aliasing
Dynamik - Signal/Rauschabstand
Quantisierungsfehler
Grundfunktionen der Audiobearbeitung (Sample-Editing)
(auch als pdf zum Offline-Lesen
und Drucken)
Begriffe
Ein Ton ist eine Schwingung, die durch periodische Regelmäßigkeit eine definierbare Grundfrequenz - die Tonhöhe - hörbar werden läßt. Der Klang eines Tons hängt von den Anteilen weiterer Schwingungen innerhalb der Grundschwingung ab. Ein Geräusch - etwa einer Rassel - hat dagegen keine periodische Grundschwingung, die Luftdruckschwankungen verlaufen so unregelmäßig, daß keine Tonhöhe definierbar ist. Die Übergänge zwischen Ton und Geräusch sind fließend, denkt man daran, daß sich Konzertpauken sehr wohl stimmen lassen, obwohl sie als perkussive Instrumente bereits sehr diffuse Klangspektren erzeugen.
Sound wird heute oft im 'Multimedia-Deutsch' für alles, was mit dem Audiobereich zu tun hat verwendet. Zum Teil geschieht das sicher aus Unkenntnis der Begriffe aus Akustik und Musik. Der Begriff Sound hat jedoch auch Vorteile, da er problematische Fragen der traditionellen Begriffe und Wissenschaftsdisziplinen ausblendet (Was ist Musik?!).
Sprache ist danach ein geräuschhaftes=nichtperiodisches Klangereignis,
das durch seine definierten Frequenzgemische sprachliche Lautmuster enthält.
Im Gesang werden diese Lautmuster einer periodischen Schwingung aufmoduliert.
Für gute Sprachverständlichkeit reicht ein Frequenzbereich bis 8 kHz vollkommen
aus.
Beispiele für Schwingungen im Audiobereich
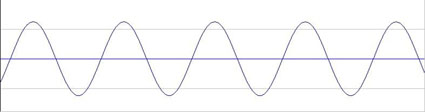
Sinuswelle - Das 'Urbild' einer periodischen Schwingung, sie besitzt keine weiteren Frequenzanteile
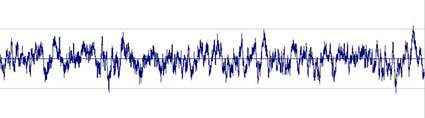
Rauschen - 'Schwingungschaos', das Gegenteil einer periodischen Schwingung
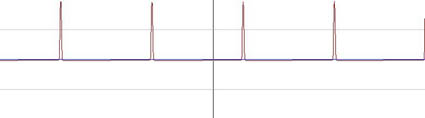
obertonreiche Schwingung - hier eine 'pulsbreitenmodulierte' Sägezahnschwingung, also ein Sägezahn, dessen Anlaufflanke verschoben und verkürzt wurde.

perkussiver Klang - hier ein metallisch klingender Synthesizerklang, dessen Tonhöhe noch deutlich wahrzunehmen ist. Eine weitere Erhöhung der Komplexität des Frequenzgemischs würde den Ton in ein Geräusch übergehen lassen.
Klang - Analyse und Synthese
'Klangfarben' sind Frequenzgemische, deren Obertonstruktur nicht den Eindruck eines Mehrklangs hervorruft - also das gleichzeitige Erklingen noch unterscheidbarer Einzeltöne -, sondern den spezifischen Klangeindruck eines Tons oder Geräuschs ausmacht. Künstlich erzeugte Standard-Wellenformen (durch Synthesizer-Hard- oder Software) haben beispielsweise folgende Obertonanteile:
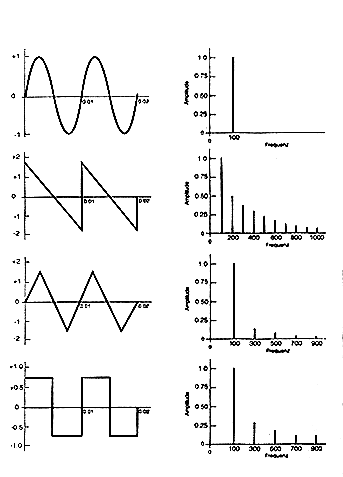
Fourieranalyse
"Der Satz von Fourier besagt zusammenfassend, dass man jede periodische Schwingung, wie kompliziert sie auch sein mag, als die Überlagerung reiner, harmonischer Schwingungen darstellen kann, deren Grundfrequenz durch die Wiederholfrequrenz der periodischen Schwingung gegeben ist." (5, Ackermann, S. 16)
Im praktischen Umgang mit Audiosignalen ist die davon abgeleitete Fast Fourier Transformation (FFT) von Bedeutung, mit welcher der spektrale Aufbau (Amplitudenspektrum) des zu analysierenden Audiosignals berechnet werden kann.
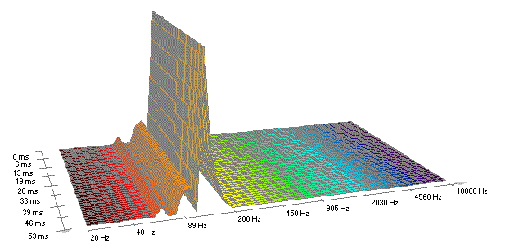
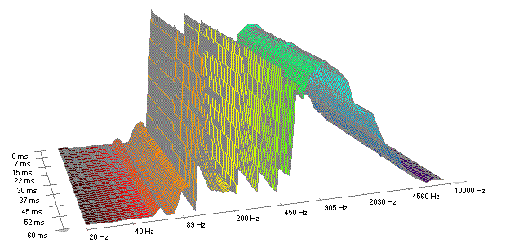
'pulsbreitenmodulierte' Sägezahnschwingung
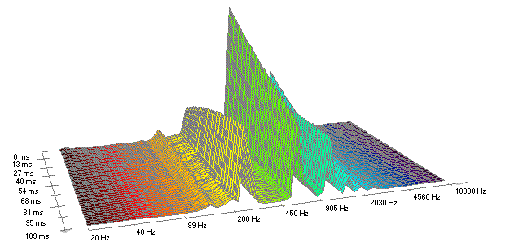
perkussiver Klang (kurz nach dem Anschlag)
Naturinstrumente erzeugen typische Frequenzspektren durch ihre physischen Resonanzen
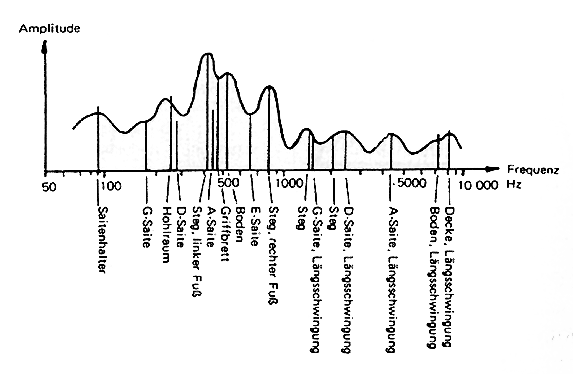
Erzeugung von Frequenzanteilen bei einer Geige
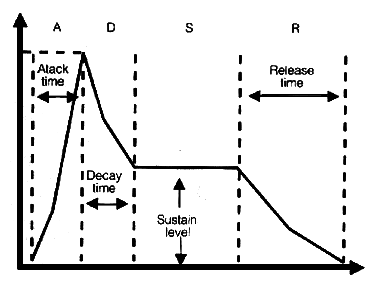
Hüllkurve
'Hüllkurve' nennt man den Zeitverlauf zentraler Parameter innerhalb
eines Tons oder Geräuschs. Die wichtigsten Parameter sind bei elektronisch
erzeugten bzw. bearbeiteten 'Sounds' die Amplitude (Lautstärke) und Filtereinstellungen.
Audiodaten - MIDI-Daten
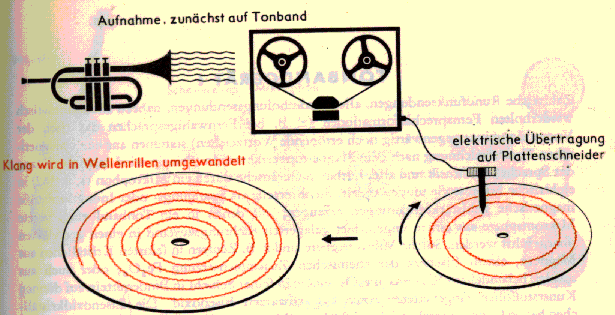
Audiodaten bilden Luftdruckschwankungen ab. Da diese zunächst in elektrische Spannungsschwankungen umgesetzt werden, codieren sie präzise gesagt einen elektrischen Spannungsverlauf in den Parametern Amplitude/Zeit.
Abbildungsaspekt des Mediums
Vom herkömmlichen Verständnis ein Medium (im Sinne von Über-
bzw. Vermittlung): 'Abbildung' eines Phänomens auf einen Träger und Reproduktion.
Shannon/Weavers Modell der Signalübertragung
verdeutlicht diesen Aspekt
intermedial vergleichbar mit:
Pixelorientierung bei Bildmedien (Fotografie, Bitmap)
Abbildungen von Schrift bei Textmedien (Kopierer, FAX)
spezifische Fehler: Knackser, Rauschen, Dynamikprobleme

weitere Beispiele:
Automatophonisches
Klavier
mechanische Musikantin
Übertragung einer Komposition
auf Stiftwalzen
MIDI-Daten sind Steuerungsdaten = Anweisungen zur Generierung von Klängen (auch Notation)
Generativer Aspekt des Mediums, im musikalischen Sinne sein 'Instrumentcharakter'
Vom herkömmlichen Verständnis her ein automatischer Generator; statt Abbildung/Übertragung steht ein generatives Moment im Vordergrund. Erst ein neueres Medienverständnis zählt auch generative Aspekte zu den Eigenschaften aller Medien und gewichtet das Verhältnis von Abbildung und Produktion neu.
intermedial vergleichbar mit:
Objektorientierung (Zerlegung in geometrische
Grundformen; Vektorgrafik) bei Bildmedien
digitale Codierung des Alphabets bei Textmedien (ASCII;
Word Processing)
spezifische Probleme: mechanischer Rhythmus und Klang, Totalaussetzer
Die "Guidonische Hand" zeigt, dass auch die Vorformen der Notenschrift etwas 'Digitales' im engeren Sinne des Wortes haben.
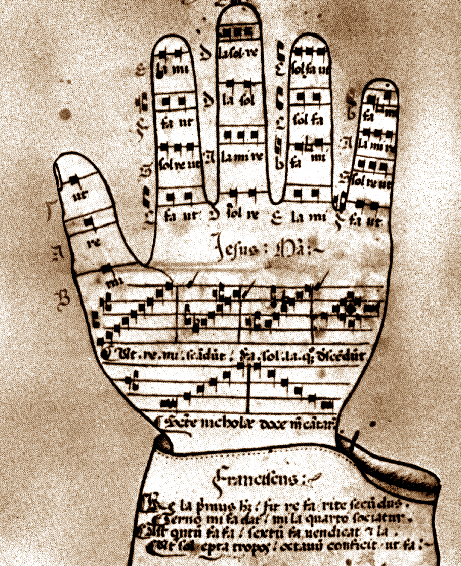
Guido von Arezzo (ca. 992-1050) führte mit den Solmisationsilben
ein Zeichensystem relativer Tonverhältnisse ein, das dem Chor durch
eine Fingersprache vermittelt werden konnte. Die Silben bilden die Versanfänge
eines Johannes-Hymnus:
Ut queant laxis Damit mit lockerem
Ansatz
Resonare fibris singen können
Mira gestorum von den Wundern
Deines Tuns
Famuli tuorum die Schüler
Solve polluti löse
der sündhaften
Labii reatum Lippen
Fehl
Sancte Johannes Heiliger Johannes
Digitalisierung
Die Digitalisierung von Audiodaten erfordert eine A/D- (und natürlich am Ende des Prozesses eine D/A) Wandlung. Beim Wintel PC macht dies die 'Soundkarte', Apple-Rechner verfügen als 'Multimedia'-Pioniere bereits seit längerer Zeit über eingebaute und ins Betriebssystem integrierte Wandlerhardware. Der zur Zeit allgemein verfügbare 'Standard' für die Audiohardware ist eine Digitalisierung in 'Zeitscheiben' von 44,1 kHz und einer 'Lautstärkerasterung' von 16 bit.

Jeder dieser Balken visualisiert einen diskreten Meßwert (ein Sample in der technischen Definition). Die gezackte Begrenzungslinie entspricht in Annäherung dem kontinuierlichen Verlauf der Welle.
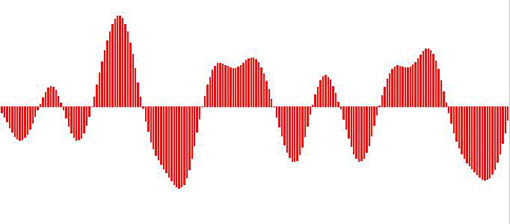
Quantisierung einer komplexeren Schwingung
Dieses Verfahren heißt in der Fachsprache Pulse-Code-Modulation (PCM). In der Praxis wird statt der jeweiligen Abtastwerte oft nur die Differenz zur letzten Messung (Differential PCM), oder die Richtung des nächsten Werts (Delta-Modulation, 1-bit Wandlung) bestimmt, bevor zum Standard-Datenformat transformiert wird.
Funktionselemente der Hardware
Soundkarten oder entsprechende Baugruppen bei integrierten Systemen ermöglichen die Ein- und Ausgabe von Audio- und MIDI-Daten. Das folgende Bild gibt - als Erinnerung an das schöne Tafelbild der Sitzung - einen rudimentären Eindruck der Anschlüsse und Signalwege einer üblichen Soundkarte.

Datenübertragung und Speicherung
für Audiodaten richtet sich nach den allgemeinen Möglichkeiten für Speicherung auf Festplatten, CD-ROMS, Wechselmedien etc. und Netzübertragung (AppleTalk, Ethernet, SCSI). Dabei sind Hardware (Speicher- und Übertragungskapazität) und Software (Cacheorganisation und Protokolle) zu berücksichtigen. Sind Audiodaten erst einmal digitalisiert, unterscheiden sie sich um nichts von ihren Text- oder Bild-'Kollegen'. Das Einzelmedium ist im digitalen Medium 'aufgegangen'.
Die Datenrate, die dabei pro Sekunde und Kanal anfällt, entspricht der Sampleauflösung mal der Samplefrequenz.
Beim üblichen Format (CD-Standard): Stereo, 44,1 kHz, 16 Bit ergeben sich:
2 x 44100 x 16 = 1.411.200 Bit/s oder 176.400 Byte/s oder 172,26 KByte/s.
Übertragungsraten für andere Auflösungen und Samplefrequenzen (unkomprimiert):
| 44,1 kHz | 22 kHz | 11 kHz | |
| 16 Bit | 172 KByte/s | 88 KByte/s | 44 KByte/s |
| 12 Bit | 132 KByte/s | 66 KByte/s | 33 KByte/s |
| 8 Bit | 88 KByte/s | 44 KByte/s | 22 KByte/s |
Übertragungsraten (komprimiert):
Typische Performance Daten von MPEG-1 Layer III
| sound quality | bandwidth | mode | bitrate | reduction ratio |
| "telephone sound" | 2.5 kHz | mono | 8 Kbps | 96:1 |
| "better than shortwave" | 4.5 kHz | mono | 4.5 kHz | 48:1 |
| "better than AM radio" | 7.5 kHz | mono | 32 Kbps | 24:1 |
| "similar to FM radio" | 11 kHz | stereo | 56...64 Kbps | 26...24:1 |
| "near CD" | 15 kHz | stereo | 96 Kbps | 16:1 |
| "CD" | 15 kHz | stereo | 112..128 Kbps | 14..12:1 |
Faustregeln für den Bedarf an Speicherplatz:
Pro Minute werden bei unkomprimierten Daten (Stereo, 44,1 kHz, 16 bit)
ca. 10 MByte Speicherplatz benötigt,
bei stark komprimierten Daten (Real Audio, MPEG-1/Layer 3) ca. 1 MByte.
Spitzfindigkeiten mit bits und Bytes:
1 Byte = 8 bit (ein 'Datenwort')
Die Präfixe Kilo (K) und Mega (M), die im Normalgebrauch den Faktor 1.000 bzw. 1.000.000 bezeichnen, richten sich im Bereich der bits und Bytes nach den 2er-Potenzen des binären Systems. Dort gilt also:
1 kbit = 1000 bit (Ausnahme mit kleinem k)
1 Kbit = 1024 bit = 128 Byte
1 Mbit = 1024x1024 bit = 1048576 bit = 131072 Byte = 128 KByte
Audiodatenformate
Unkomprimierte Formate:
.wav (MS-Windows-Format)
.aiff (audio interchange file format; auf Apple-Plattformen üblich)
Apple System 7 Sounds (.snd)
Spezialformate:
.voc (Creative Labs)
.sd/.sd2 (Sound Designer)
Komprimierte Formate / Internet:
.ra/.ram (Real Audio)
.mp3/.m3u (MPEG-1, Layer 3)
Aussteuerung
Eine möglichst gute Aussteuerung des Aufnahmepegels ist die Voraussetzung für eine rauscharme und dynamikreiche A/D Wandlung. Anders als bei analogen Aufnahmeverfahren, für die diese Regel ebenfalls gilt, gibt es allerdings bei der Digitalisierung keinen Grenzbereich, sondern eine genau definierte obere Pegelgrenze, bei deren Überschreiten keine Abbildung der Wellenform mehr möglich ist. Es wird solange nur ein Wert (der Höchstwert) gemessen, wie der zulässige Pegel überschritten wird. Resultat ist eine 'gekappte' Welle, die sich einer Rechteckschwingung annähert und mit dem Original kaum noch etwas gemeinsam hat.
Interferenz
Überlagerung zweier oder mehrerer Schwingungen mit dem Ergebnis von Interferenzschwingungen (Schwebungen)
Die Digitalisierung kontinuierlicher Phänomene wie Bilder und Töne ist
prinzipiell mit einer Rasterung verbunden. Dabei können sich die Rasterfrequenz
und eine wellenförmige Struktur des Gegenstands überlagern und weitere,
vorher nicht existente Schwingungen ergeben. Interferenzprobleme bei der
Digitalisierung treten aus zwei Ursachen auf:
- das zu digitalisierende Phänomen hat selbst eine 'natürliche' Wellenstruktur,
wie etwa die Luftschwingungen des Schalls oder sich periodisch bewegende
Gegenstände im Bewegtbild oder
- ein 'naturgemäß' unperiodisches Phänomen wurde durch Medientransformationen
bereits gerastert.
Aliasing
Beim Digitalisieren können Frequenzen entstehen, die im Original nicht vorhanden sind. Diese Artefakte oder 'Aliasfrequenzen' des Digitalisierungsvorgangs sind Ergebnisse einer unzureichenden Abtastfrequenz. Auch hier gilt - wie bei jedem Wellenphänomen und beim Bild bereits besprochen - das Nyquist/Shannon-Theorem: Die Abtastrate muß mindestens das Doppelte der zu digitalisierenden Frequenz betragen.
Da in Audiosignalen immer - ob gewünscht oder nicht - hochfrequente Anteile vorhanden sind, die jede Datenrate und Speicherkapazität sprengen würden, gibt es nur zwei Lösungswege für dieses Problem (i.d.R. kombiniert angewandt):
Filterung - im Audiosignal werden alle Frequenzen über der beabsichtigten halben Digitalisierungsfrequenz herausgefiltert. Es ist allerdings mit vertretbarem Aufwand nicht möglich, auf analogem Wege alle Frequenzen zu entfernen, sie werden lediglich gedämpft ('Q-Faktor', 'Dämpfungsfaktor', 'Flankensteilheit' des Filters).
Oversampling - das Signal wird mit einem Vielfachen (z.B. 64fach) der Abtastfrequenz abgetastet, um Aliasing zu vermeiden. Auf digitalem Weg werden dann die hohen Frequenzen herausgerechnet. Oft wird die Kombination beider Verfahren angewendet.
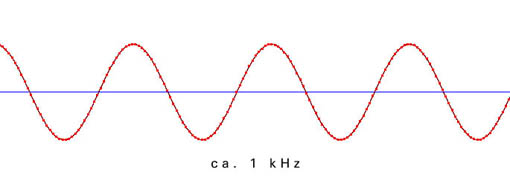
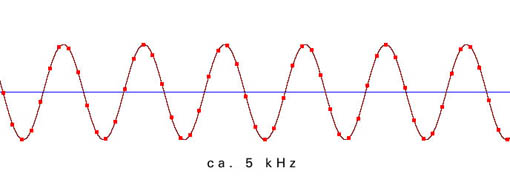
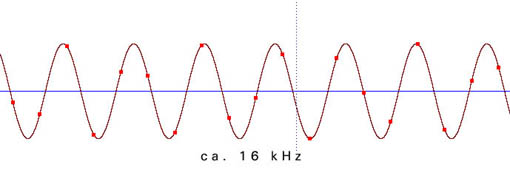
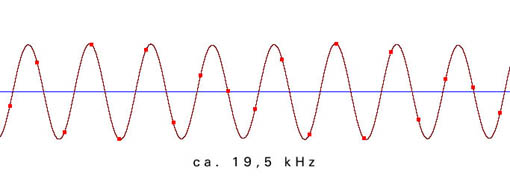
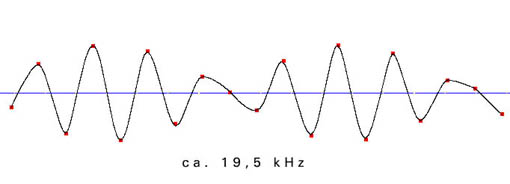
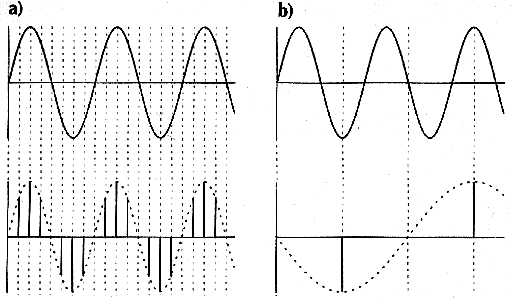
Die folgenden Beispiele zeigen die Verteilung der einzelnen Meßpunkte in Abhängigkeit von der Freqenz der zu digitalisierenden Schwingung. Die Samplingfrequenz (=zeitliche Abtastrate) beträgt bei allen Beispielen 44100 Hz.
aus der ungenauen Abtastung in der Nähe der Grenzfrequenz ergibt sich ein phasenungenaues und amplitudenverändertes Signal:
Dynamik - Signal/Rauschabstand
Die Dynamik eines Signals bezeichnet den Umfang seiner Lautstärkeunterschiede oder einfacher gesagt, sie bestimmt, wie weit sich ein Pianissimo und ein Fortissimo unterscheiden. Um die Nuancen eines Konzerts für Violine und Orchester wiederzugeben, ist eine wesentlich größere Dynamik erforderlich als etwa für eine Nachrichtensendung. Manchmal ist eine große Dynamik sogar unerwünscht, etwa in Werbeclips, die sich durch einen gleichbleibend hohen Pegel aus dem Programmumfeld herausheben sollen.Gemäß den Eigenschaften des menschlichen Gehörs wird die Dynamik in der logarithmischen Einheit Dezibel angegeben.
Der Dynamikumfang natürlicher Instrumente:
| Sprache | Sologesang | Streicher | Klavier | Orchester |
| 15-20 dB | 40-50 dB | 30-35 dB | 40-50 dB | 30-70 dB |
Um die Dynamik des Originalsignals beizubehalten, muß der Signal/Rauschabstand der Dynamik des Originalsignals mindestens entsprechen. Bei elektrischen und elektronischen Übertragungssystemen wird die technisch mögliche Dynamik als Systemdynamik bezeichnet. Sie ist als Differenz von Übersteuerungsgrenze und Rauschpegel definiert.
Systemdynamik von analogen Übertragungssystemen:
| Studioverstärker | Plattenspieler | Compakt Cassette | MW-Radio | Muzak Tape |
| 100 dB | 50 dB | 40 dB | 30 dB | 20 dB |
Die maximale Systemdynamik errechnet sich nach der Formel:
S(ignal)/N(oise) [dB] = 6,02n + 1,76
n entspricht der Länge der Binärzahl in Bit. Bei einer Auflösung von 16 Bit beträgt die maximale Systemdynamik demnach ca. 98 dB. Die tatsächlich nutzbare Dynamik und somit der effektive Signal/Rauschabstand liegt allerdings weit darunter, da ein bewerteter Störpegel von 14 dB, ein Schutzabstand zum Störpegel von 20 dB (Footroom) und eine Aussteuerungsreserve von 10 dB (Headroom) berücksichtigt werden müssen. Bei einer 16-Bit-Auflösung ergibt sich somit ein effektiver Signal/Rauschabstand von 54 dB. Dynamik [dB] = 98 - 14 - 20 -10 = 54
Quantisierungsfehler
Da das wertkontinuierliche Analogsignal bei der Digitalisierung auf Werte einer endlichen Wertemenge abgebildet wird, kommt es zu Rundungsfehlern. Da diese Fehlerbeträge im Zeitverlauf statistisch gleich verteilt auftreten, können sie als Rauschen interpretiert werden (Quantisierungsrauschen). Insbesondere bei Signalen, die in einem geradzahligen Verhältnis zur Abtastfrequenz stehen, ergibt sich ein unangenehmes 'tonales' Rauschen, da die Fehlerrate nicht mehr zufällig ist, sondern dem Phasenverhalten des Signals folgt.
Dithering
Um den signalabhängigen Klangcharakter des Quantisierungsrauschens bei geringer Aussteuerung des abzutastenden Signals zu unterdrücken, wird dem Originalsignal vor der Digitalisierung eine geringe Rauschspannung (Dither-Rauschen) beigemischt. Auch bei der Requantisierung auf digitaler Ebene wird ein Dithersignal zugesetzt, um die dabei entstehenden Fehler zu maskieren.
Literatur
Ackermann, Philipp: Computer und Musik. Eine Einführung in die digitale Klang- und Musikverarbeitung. Wien 1991
Henle, Hubert: Das Tonstudiohandbuch. Praktische Einführung in die professionelle Aufnahmetechnik. München 1998
Stotz, Dieter: Computergestützte Audio- und Videotechnik. Multimediatechnik in der Anwendung. Berlin 1995
Zander, Horst: Das PC-Tonstudio. Von der Audioaufnahme und Verarbeitung mit dem PC bis zur Master-CD. Poing 1998