
Ein Ton ist eine Schwingung, die durch periodische Regelmäßigkeit eine definierbare Grundfrequenz - die Tonhöhe - hörbar werden läßt. Der Klang eines Tons hängt von den Anteilen weiterer Schwingungen innerhalb der Grundschwingung ab. Ein Geräusch - etwa einer Rassel - hat dagegen keine periodische Grundschwingung, die Luftdruckschwankungen verlaufen so unregelmäßig, daß keine Tonhöhe definierbar ist. Die Übergänge zwischen Ton und Geräusch sind fließend, denkt man daran, daß sich Konzertpauken sehr wohl stimmen lassen, obwohl sie als perkussive Instrumente bereits sehr diffuse Klangspektren erzeugen.
Sound wird heute oft im 'Multimedia-Deutsch' für alles, was mit dem Audiobereich zu tun hat verwendet. Zum Teil geschieht das sicher aus Unkenntnis der Begriffe aus Akustik und Musik. Der Begriff Sound hat jedoch auch Vorteile, da er problematische Fragen der traditionellen Begriffe und Wissenschaftsdisziplinen ausblendet (Was ist Musik?!).
Sprache ist danach ein geräuschhaftes=nichtperiodisches Klangereignis, das durch seine definierten Frequenzgemische sprachliche Lautmuster enthält. Im Gesang werden diese Lautmuster einer periodischen Schwingung aufmoduliert.
Für gute Sprachverständlichkeit reicht ein Frequenzbereich bis 8 kHz vollkommen aus.
Beispiele für Schwingungen im Audiobereich

Sinuswelle - Das 'Urbild' einer periodischen Schwingung, sie besitzt keine weiteren Frequenzanteile

Rauschen - 'Schwingungschaos', das Gegenteil einer periodischen Schwingung

obertonreiche Schwingung - hier eine 'pulsbreitenmodulierte' Sägezahnschwingung , also ein Sägezahn, dessen Anlaufflanke verschoben und verkürzt wurde.

perkussiver Klang - hier ein metallisch klingender Synthesizerklang, dessen Tonhöhe noch deutlich wahrzunehmen ist. Eine weitere Erhöhung der Komplexität des Frequenzgemischs würde den Ton in ein Geräusch übergehen lassen.
Grundsätzlich sind Daten im Audiobereich zeitkritisch, d.h. sie stellen Anforderungen an DV-Hard- und Software, die historisch gesehen atypisch für einen 'Rechner' sind. Bis heute sind damit Geschwindigkeits-, Bandbreiten- und Speicherprobleme verbunden, die von technischen und ökonomischen Rahmenbedingungen abhängen.

Audiodaten bilden Luftdruckschwankungen ab. Da diese zunächst in elektrische Spannungsschwankungen umgesetzt werden, codieren sie präzise gesagt einen elektrischen Spannungsverlauf in den Parametern Amplitude / Zeit.
Damit Audiodaten aufgenommen und wiedergegeben werden können, werden A(nalog)/D(igital)-Wandler bzw. D/A-Wandler benötigt. Diese werden i.d.Regel von der Soundkarte zur Verfügung gestellt.
Der Datentyp ist vergleichbar mit:
Pixelorientierung bei Bildmedien (Fotografie, Bitmap)
Abbildungen von Schrift bei Textmedien (Kopierer, FAX)
spezifische Fehler: Knackser, Rauschen, Dynamikprobleme

weitere Beispiele:
Automatophonisches Klavier
mechanische Musikantin
Übertragung einer Komposition auf Stiftwalzen
MIDI-Daten sind Steuerungsdaten = Anweisungen zur Generierung von Klängen (auch Notation)
Um MIDI-Daten zum Klingen zu bringen, wird ein entsprechender Klangerzeuger (Synthesizer) benötigt. >Soundkarte
Dieser Datentyp ist vergleichbar mit:
Objektorientierung (Zerlegung in geometrische Grundformen; Vektorgrafik) bei Bildmedien
digitale Codierung des Alphabets bei Textmedien (ASCII; Word Processing)
spezifische Probleme: mechanischer Rhythmus und Klang, Timingprobleme, Totalaussetzer
Analoge Audiosignale sind kontinuierliche Signale. Bei der Digitalisierung werden diese in eine regelmäßige Folge von diskreten Werten gewandelt. Hierzu wird die Amplitude des Signals in regelmäßigen Abständen abgetastet und den einzelnen Stichproben (=Samples) Werte aus einer begrenzten Wertemenge zugeordnet (Quantisierung). Dabei wird ein Raster verwendet, dass die möglichen Werte bestimmt. Die Abtastfrequenz (=Abtastrate, Abtastfrequenz, Samplefrequenz, Samplerate; in Hz oder kHz angegeben) bestimmt, wie oft das Signal pro Sekunde abgetastet wird. Die Auflösung (=Quantisierung; in bit angegeben) legt die mögliche Wertemenge pro Sample fest.
Die Digitalisierung von Audiodaten erfordert eine A/D- (und natürlich am Ende des Prozesses eine D/A) Wandlung . Beim Wintel PC macht dies die 'Soundkarte', Apple-Rechner verfügen als 'Multimedia'-Pioniere bereits seit längerer Zeit über eingebaute und ins Betriebssystem integrierte Wandlerhardware. Der zur Zeit allgemein verfügbare 'Standard' für die Audiohardware ist eine Digitalisierung in 'Zeitscheiben' von 44,1 kHz und einer 'Lautstärkerasterung' von 16 bit.

Jeder dieser Balken visualisiert einen diskreten Meßwert (ein Sample in der technischen Definition). Die gezackte Begrenzungslinie entspricht in Annäherung dem kontinuierlichen Verlauf der Welle.
Soundkarten oder entsprechende Baugruppen bei integrierten Systemen ermöglichen die Ein- und Ausgabe von Audio- und MIDI-Daten. Das folgende Bild gibt einen rudimentären Eindruck der Anschlüsse und Signalwege einer üblichen Soundkarte.

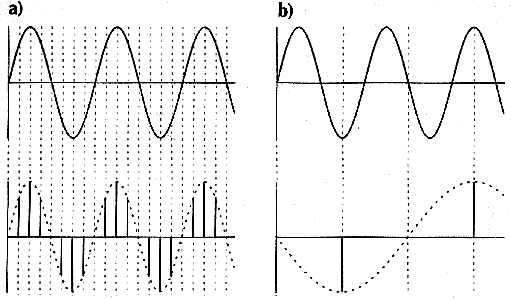
Eine möglichst gute Aussteuerung des Aufnahmepegels ist die Voraussetzung für eine rauscharme und dynamikreiche A/D Wandlung. Anders als bei analogen Aufnahmeverfahren, für die diese Regel ebenfalls gilt, gibt es allerdings bei der Digitalisierung keinen Grenzbereich, sondern eine genau definierte obere Pegelgrenze, bei deren Überschreiten keine Abbildung der Wellenform mehr möglich ist. Es wird solange nur ein Wert (der Höchstwert) gemessen, wie der zulässige Pegel überschritten wird. Resultat ist eine 'gekappte' Welle, die sich einer Rechteckschwingung annähert und mit dem Original kaum noch etwas gemeinsam hat.
Beim Digitalisieren können Frequenzen entstehen, die im Original nicht vorhanden sind. Diese Artefakte oder 'Aliasfrequenzen' des Digitalisierungsvorgangs sind Ergebnisse einer unzureichenden Abtastfrequenz. Auch hier gilt - wie bei jedem Wellenphänomen und beim Bild bereits besprochen - das Nyquist/Shannon-Theorem: Die Abtastrate muß mindestens das Doppelte der zu digitalisierenden Frequenz betragen.
Da in Audiosignalen immer - ob gewünscht oder nicht - hochfrequente Anteile vorhanden sind, die jede Datenrate und Speicherkapazität sprengen würden, gibt es nur zwei Lösungswege für dieses Problem (i.d.R. kombiniert angewandt):
Filterung - im Audiosignal werden alle Frequenzen über der beabsichtigten halben Digitalisierungsfrequenz herausgefiltert. Es ist allerdings mit vertretbarem Aufwand nicht möglich, auf analogem Wege alle Frequenzen zu entfernen, sie werden lediglich gedämpft ('Q-Faktor', 'Dämpfungsfaktor', 'Flankensteilheit' des Filters).
Oversampling - das Signal wird mit einem Vielfachen (z.B. 64fach) der Abtastfrequenz abgetastet, um Aliasing zu vermeiden. Auf digitalem Weg werden dann die hohen Frequenzen herausgerechnet. Oft wird die Kombination beider Verfahren angewendet.
Die Dynamik eines Signals bezeichnet den Umfang seiner Lautstärkeunterschiede oder einfacher gesagt, sie bestimmt, wie weit sich ein Pianissimo und ein Fortissimo unterscheiden. Um die Nuancen eines Konzerts für Violine und Orchester wiederzugeben, ist eine wesentlich größere Dynamik erforderlich als etwa für eine Nachrichtensendung. Manchmal ist eine große Dynamik sogar unerwünscht, etwa in Werbeclips, die sich durch einen gleichbleibend hohen Pegel aus dem Programmumfeld herausheben sollen. Gemäß den Eigenschaften des menschlichen Gehörs wird die Dynamik in der logarithmischen Einheit Dezibel angegeben.
Der Dynamikumfang natürlicher Instrumente:
| Sprache | Sologesang | Streicher | Klavier | Orchester |
| 15-20 dB | 40-50 dB | 30-35 dB | 40-50 dB | 30-70 dB |
Um die Dynamik des Originalsignals beizubehalten, muß der Signal/Rauschabstand der Dynamik des Originalsignals mindestens entsprechen. Bei elektrischen und elektronischen Übertragungssystemen wird die technisch mögliche Dynamik als Systemdynamik bezeichnet. Sie ist als Differenz von Übersteuerungsgrenze und Rauschpegel definiert.
Systemdynamik von analogen Übertragungssystemen:
| Studioverstärker | Plattenspieler | Compakt Cassette | MW-Radio | Muzak Tape |
| 100 dB | 50 dB | 40 dB | 30 dB | 20 dB |
Sample-Editoren
dienen zur Bearbeitung von Audiodat(ei)en. (s.u.)
Sequenzer
waren zunächst reine MIDI-Anwendungen (Sequenz=Tonfolge), entwickelten sich jedoch in den letzten Jahren zu universellen und hochkomplexen Werkzeugen der digitalen Musikproduktion. Sie integrieren MIDI- und Audio-Daten in einem gemeinsamen Arrangement und übernehmen die zeitliche Synchronisation beider Datentypen. Darüberhinaus stellen sie die wichtigsten Bearbeitungsmöglichkeiten bis hin zur Einbindung von Effekten und Steuerparametern für Klangerzeuger zur Verfügung.
Tools
vom RealPlayer bis zum MPEG-Encoder werden immer mehr verwendet. Auch 'Spielereien' wie Software-Synthesizer und Visualisierungen von Musik sind beliebt. Die Palette von Free- und Shareware ist unüberschaubar, das Internet lädt zum Experimentieren ein ...
Je nach Ziel der Bearbeitung, etwa Aufbereitung einer Audiodatei für eine Multimedia-Anwendung oder musikalische Gestaltung von 'Rohmaterial', können verschiedene Abfolgen von Arbeitsschritten sinnvoll sein. Dennoch soll die Reihenfolge der hier genannten Verfahren eine Orientierung für die Folge in der Praxis geben.
Die Pegel jedes Meßpunktes werden gleichmäßig soweit angehoben, bis die höchsten Pegel den voreingestellten Maximalwert erreichen. Damit wird zwar prinzipiell keine Dynamik gewonnen, jedoch Rauschen und Klangprobleme durch die bessere Ansteuerung von Peripheriegeräten vermieden.
Normalisieren ist außerdem für viele weitere Rechenschritte mit digitalisiertem Material günstig, da Rundungsfehler bei Rechenoperationen mit größeren Werten weniger ins Gewicht fallen.
Nach pegelverändernden Operationen kann erneutes Normalisieren sehr sinnvoll sein.
Wie aus der Text- und Bildbearbeitung bekannt, kann im Wave-Editor Audiomaterial geschnitten werden:
Cut: Ausschneiden
Copy: Kopieren in die Zwischenablage
Paste: Einfügen der Daten aus der Zwischenablage
Trim/Crop: Freistellen des ausgewählten Bereichs
Es sollte darauf geachtet werden, immer in den Nulldurchgängen zu schneiden, so daß keine Knackser entstehen. Bei Stereosignalen kann die Suche nach einem gemeinsamen Nulldurchgang beider Signale ein wenig kniffelig sein...
Durch Wiederholen eines bestimmten Segments (oder auch des gesamten Materials) entsteht ein Loop. Dieser kann z.B. dazu benutzt werden, die quasistationäre (Sustain-)Phase eines Klanges zu verlängern oder um eine ständige Rhythmusspur (Drumloop) zu erzeugen. Bei Multimedia-Anwendungen kann so Speicherplatz gespart und die Performance verbessert werden.
sind sowohl für die ästhetische Gestaltung wie auch für die einfache Aufbereitung von Daten wichtig. So kann etwa die Sprachverständlichkeit vor einem Resampling verbessert werden, oder es können störende Resonanzen des Aufnahmeraums oder der Mikrophonierung beseitigt werden.
Der Kompressor macht - einfach gesagt - ein lautes Signal leiser und ein leises Signal lauter. Die Dynamik eines Signalverlaufs wird so 'zusammengedrückt'. Für Anwendungen mit niedrigerer Dynamik als die der Originalaufnahme bieten sich Kompressoren an, um das Feld der dynamischen Bandbreite zu kontrollieren. Auch vor der Verminderung der Bitrate (z.B. 16 bit nach 8 bit für Multimedia- oder für Internetanwendungen kann durch gezielte Kompression Klangqualität 'gerettet' werden.
Die 'Lautheit' eines Signals in einem Umfeld läßt sich ebenfalls mit Kompressoren steuern. Stark komprimierte Signale können einen gleichbleibend hohen Pegel erhalten und heben sich so aus einem normalen dynamischen Umfeld heraus (>Werbung).
Ein Limiter dient zur Begrenzung von Signalpegeln ab einer definierten Grenze, sodass Übersteuerungen und Überlastungen verhindert werden können.
DAT und CD, Multimedia und Internet haben ihre eigenen anwendungsbezogenen Auflösungen, Samplingfrequenzen und Datenraten. Mit Resamplen ist die Umwandlung der Samplingfrequenz bei gleichbleibender Tonhöhe gemeint, also ein Rechenvorgang, der die vorhandenen Werte auf einen neuen Wertebereich abbildet. Je nach Umwandlung kann dabei ein komplexer Rechenvorgang notwendig werden. So ist ein Resampling von 44100 Hz auf 22050 Hz durch Wegfall jedes zweiten Wertes problemlos möglich, eine Wandlung von 22050 Hz auf 48000 Hz erfordert dagegen die 2,176870748299fache Wertemenge mit entsprechender Interpolation der Samplewerte. Neben dem längeren Rechenvorgang kann außerdem Quantisierungsrauschen entstehen.
Es ist daher immer sinnvoll, vor einer Aufnahme oder A/D-Wandlung eine dem Verarbeitungszweck entsprechende Samplingfrequenz zu wählen.
Eine Zumischung des zeitverzögerten Originals erzeugt je nach Verzögerungszeit folgende Effekte:
ca. 0-30 ms Raumorientierung, Phasing, Chorus
ca. 20-100 ms Dopplungseffekte (Delay)
>100ms Hall (Mehrfachverzögerungen mit Zeiten bis in den Bereich mehrerer Sekunden)
Verrauschte oder gestörte Aufnahmen lassen sich mit verschiedenen Verfahren verbessern. Ein Noise-Gate entfernt low-level Geräusche, ein 'echter' Denoiser nimmt ein Rauschmuster aus der Datei und senkt die entsprechenden Frequenzbänder ab.
Für Multimedia-Anwendungen sind Ein- und Ausblenden als abschließendes Verfahren wichtige Gestaltungsmittel.
für Audiodaten richtet sich nach den allgemeinen Möglichkeiten für Speicherung auf Festplatten, CD-ROMS, Wechselmedien etc. und Netzübertragung (AppleTalk, Ethernet, SCSI). Dabei sind Hardware (Speicher- und Übertragungskapazität) und Software (Cacheorganisation und Protokolle) zu berücksichtigen.
Die Datenrate, die dabei pro Sekunde und Kanal anfällt, entspricht der Sampleauflösung mal der Samplefrequenz.
Beim üblichen Format (CD-Standard): Stereo, 44,1 kHz, 16 Bit ergeben sich:
2 x 44100 x 16 = 1.411.200 Bit/s oder 176.400 Byte/s oder 172,26 KByte/s .
Übertragungsraten für andere Auflösungen und Samplefrequenzen (unkomprimiert):
| 44,1 kHz | 22 kHz | 11 kHz | |
| 16 Bit | 172 KByte/s | 88 KByte/s | 44 KByte/s |
| 12 Bit | 132 KByte/s | 66 KByte/s | 33 KByte/s |
| 8 Bit | 88 KByte/s | 44 KByte/s | 22 KByte/s |
Zur Senkung der erforderlichen Übertragungs-Bandbreite und Speicherkapazität werden verschiedene Verfahren der Datenreduktion bzw. -komprimierung verwendet. Zu unterscheiden ist zwischen der verlustfreien und verlustbehafteten Komprimierung.
Die verlustfreie Komprimierung (z.B. ZIP, ARC), bei der die Originaldaten vollständig wiederhergestellt werden können, nutzt statistisch-informationstheoretische Redundanzen zur Minimierung des Datenaufkommens.
Verlustbehaftete Komprimierung wertet die wahrnehmungsphysiologische und pychoakustische Relevanz von Signalen aus und entfernt irrelevante Anteile (etwa bei Verdeckungsphänomenen). Konsumergeräte (MiniDisc) und Internetanwendungen (Real Audio, MPEG) nutzen diese Variante der Komprimierung.
Übertragungsraten (komprimiert):
Typische Performance Daten von MPEG-1 Layer III
| sound quality | bandwidth | mode | bitrate | reduction ratio |
| "telephone sound" | 2.5 kHz | mono | 8 Kbps | 96:1 |
| "better than shortwave" | 4.5 kHz | mono | 4.5 kHz | 48:1 |
| "better than AM radio" | 7.5 kHz | mono | 32 Kbps | 24:1 |
| "similar to FM radio" | 11 kHz | stereo | 56...64 Kbps | 26...24:1 |
| "near CD" | 15 kHz | stereo | 96 Kbps | 16:1 |
| "CD" | 15 kHz | stereo | 112..128 Kbps | 14..12:1 |
Faustregeln für den Bedarf an Speicherplatz:
Pro Minute werden bei unkomprimierten Daten (Stereo, 44,1 kHz, 16 bit) ca. 10 MByte Speicherplatz benötigt,
bei stark komprimierten Daten (Real Audio, MPEG-1/Layer 3) ca. 1 MByte.
Audiodatenformate
Unkomprimierte Formate:
.wav (MS-Windows-Format)
.aiff (audio interchange file format; auf Apple-Plattformen üblich)
Komprimierte Formate / Internet:
.ra/.ram (Real Audio)
.mp3/.m3u (MPEG-1, Layer 3)
Spitzfindigkeiten mit bits und Bytes:
1 Byte = 8 bit (ein 'Datenwort')
Die Präfixe Kilo (K) und Mega (M), die im Normalgebrauch den Faktor 1.000 bzw. 1.000.000 bezeichnen, richten sich im Bereich der bits und Bytes nach den 2er-Potenzen des binären Systems. Dort gilt also:
1 kbit = 1000 bit (Ausnahme mit kleinem k)
1 Kbit = 1024 bit = 128 Byte
1 Mbit = 1024x1024 bit = 1048576 bit = 131072 Byte = 128 KByte