

Als Luft-Hörschall werden Luftdruckschwankungen bezeichnet, die über das menschliche Ohr wahrnehmbar sind. Diese breiten sich in Form einer Longitudinalwelle räumlich um die Schallquelle aus und können lokal als Schwingung interpretiert werden. Aus der Schwingungslehre entstammen dann auch die grundlegenden Begriffe Amplitude, Frequenz und Wellenform.
Als Gehör versteht man die "Gesamtheit aller Funktionsteile, welche zur Entstehung der als Hören bezeichneten Empfindung beitragen" (1, Rieländer, S. 110). Dazu zählen neben dem Ohr selbst auch jene Teile des Gehirns, die "...in einem komplizierten kognitiven Prozeß die ankommenden Signale als Worte, Musik, Lärm und so weiter" (2, Ackermann, S. 7) interpretieren.
Die Terminologie in der Akustik und der Musik unterscheidet sich (4, vgl. Rieländer, S. 163):
| Akustik | Musik |
| Ton, Sinuston, reiner Ton, einfacher Ton | Ton |
| Klang, einfacher Klang, harmonischer Klang | Ton |
| Klanggemisch, Mehrfachklang, Zusammenklang | Klang |
Im folgenden wird hier die Terminologie der Akustik verwendet.
Sinuston
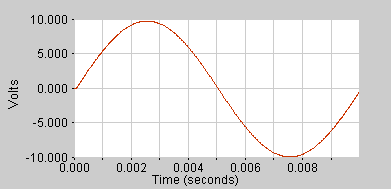
Die einfachste Form einer Schallschwingung. Es liegt nur eine diskrete Frequenz vor.
Ein einfacher (harmonischer) Klang ist eine periodische Schwingung, die aus einer Grundschwingung und mehreren Teilschwingungen besteht, deren Frequenzen harmonisch zur Grundschwingung sind, also ganzzahlige Vielfache der Frequenz der Grundschwingung. Die empfundene Tonhöhe entspricht der Frequenz der Grundschwingung. Die empfundene Klangfarbe ist durch das Obertonspektrum (die Zusammensetzung und Amplituden der Partialtöne) bedingt.
Sägezahnschwingung (Saw)
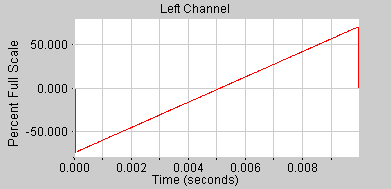
Die Sägezahnschwingung beinhaltet alle Partialtöne.
Die Amplitude der einzelnen Partialtöne berechnet sich durch:
A(n) = 1/n
Wobei n der Nummer des Partialtons entspricht.
Rechteckschwingung (Square)
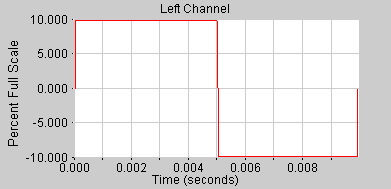
Die Rechteckschwingung beinhaltet alle ungeradzahligen Partialtöne.
Die Amplituden der einzelnen Partialtöne verhalten sich wie die der Sägezahnschwingung.
Dreieckschwingung (Triangle)
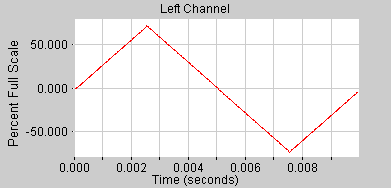
Die Dreieckschwingung beinhaltet alle ungeradzahligen Partialtöne.
Die Amplitude der einzelnen Partialtöne berechnet sich durch:
A(n) = 1/n2
Wobei n der Nummer des Partialtons entspricht.
Ein Geräusch ist ein Schallereignis mit zahlreichen Teilfrequenzen, zwischen denen kein gesetzmäßiger Zusammenhang besteht. Die Schwingung ist nicht periodisch, es kann keine Tonhöhe bestimmt werden.
Das dynamische Verhalten eines akustischen Ereignisses im Zeitverlauf kann durch eine Hüllkurve beschrieben werden. Die komplexe Hüllkurve von natürlichen Klängen kann durch einen sog. ADSR-Hüllkurve angenähert werden.
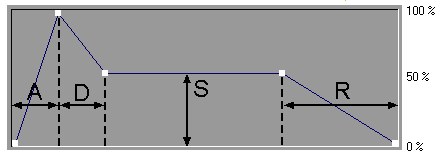
| Attack | Dauer des ersten Abschnitts der Einschwingphase bis zum Erreichen des Zeitpunktes größter Schallintensität |
| Decay | Dauer des zweiten Abschnitts der Einschwingphase zwischen dem Erreichen des Zeitpunktes größter Schallintensität und dem Erreichen des Sustain-Levels |
| Sustain | Pegel des Klangs in seiner stationären Phase (Quasistationärer Klangabschnitt) |
| Release | Dauer der Ausklingphase |
Wird die oben dargestellte Hüllkurve auf ein Audiosignal mit konstantem Pegel angewendet, ergibt sich folgendes Oszillogramm:
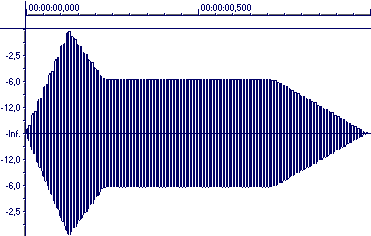
"Der Satz von Fourier besagt zusammenfassend, daß man jede periodische Schwingung, wie kompliziert sie auch sein mag, als die Überlagerung reiner, harmonischer Schwingungen darstellen kann, deren Grundfrequenz durch die Wiederholfrequrenz der periodischen Schwingung gegeben ist." (5, Ackermann, S. 16)
Im praktischen Umgang mit Audiosignalen ist die davon abgeleitete Fast Fourier Transformation (FFT) von Bedeutung, mit welcher der spektrale Aufbau (Amplitudenspektrum) des zu analysierenden Audiosignals berechnet werden kann. Bei der Analyse wird ein zeitliches Fenster betrachtet, wobei an den Rändern des Fensters Fehler auftreten, die zu Meßungenauigkeiten führen können. Deshalb werden verschiedene Fensterarten verwendet, welche die Meßungenauigkeiten bei bestimmten Signale minimieren.
| Fensterfunktion | Frequenzauflösungs- genauigkeit |
Amplituden- genauigkeit |
| Rechteck | sehr gering | groß |
| Dreieck, Bartel, Parsen | gering | groß |
| Hamming, Hanning, Blackmann, Blackmann-Harris | mittel | mittel |
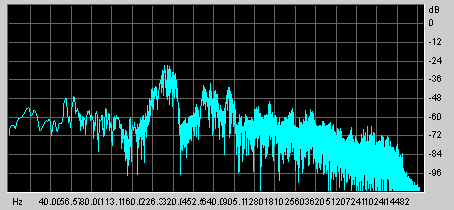
(Ergebnis einer Frequenzanalyse mit dem Programm CoolEdit96)
Um die Entwicklung des Amplitudenspektrums eines Signals im Zeitverlauf darzustellen, werden die Amplitudenspektren von kurzen Zeitabschnitten analysiert und daraus eine dreidimensionale Darstellung errechnet:
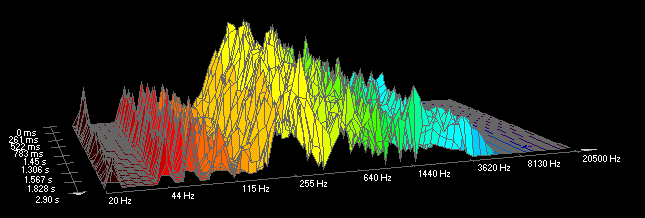
(Das gleiche Signal wie oben, analysiert mit dem Programm Wavelab 1.6)
Als Dynamik bezeichnet man den Unterschied zwischen der größten und der kleinsten Schallintensität in einem bestimmten Zeitabschnitt. Gemäß den Eigenschaften des menschlichen Gehörs wird die Dynamik in der logarithmischen Einheit Dezibel angegeben.
Dynamikumfang natürlicher Instrumente
| Sprache | Sologesang | Streicher | Klavier | Orchester |
| 15-20 dB | 40-50 dB | 30-35 dB | 40-50 dB | 30-70 dB |
Bei elektrischen und elektronischen Übertragungssystemen wird die technisch mögliche Dynamik als Systemdynamik bezeichnet. Sie ist als Differenz aus Übersteuerungsgrenze und Rauschpegel definiert.
Systemdynamik analoger Übertragungssysteme
| Studioverstärker | Plattenspieler | Compakt Cassette | MW-Radio | Muzak Tape |
| 100 dB | 50 dB | 40 dB | 30 dB | 20 dB |
Auditive Gestaltung
Großmann | SoSe 2018 | Di 14:15-15:45 | 5.326 UC
Quelle: http://audio.uni-lueneburg.de/seminarwebseiten/auditges/site1.php, 10.03.2026