

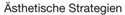
Analoge Audiosignale sind zeit- und wertkontinuierliche Signale. Bei der Digitalisierung (=Abtastung) werden diese in ein zeit- und wertdiskretes Digitalsignal umgesetzt. Hierzu wird die Amplitude des Signals in regelmäßigen Abständen abgetastet und den einzelnen Stichproben (=Samples) Werte aus einer begrenzten Wertemenge zugeordnet (Quantisierung).
Die Abtastfrequenz (=Abtastrate, Sampling-Frequenz, Sample Rate) bestimmt, wie oft das Signal pro Sekunde abgetastet wird. Die Auflösung legt die Wertemenge fest.
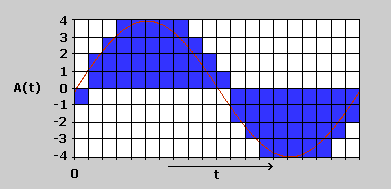
| 44,1 kHz | 22 kHz | 11 kHz | |
| 16 Bit | 176 KByte/s | 88 KByte/s | 44 KByte/s |
| 12 Bit | 132 KByte/s | 66 KByte/s | 33 KByte/s |
| 8 Bit | 88 KByte/s | 44 KByte/s | 22 KByte/s |
Als Faustformel gilt: Eine Audiodatei mit einer Auflösung von 16 Bit und einer Abtastrate von 44,1 kHz, Stereo (CD-Qualität) hat eine Größe von etwa 10 MByte pro Minute.
Das von Shannon formulierte Abtasttheorem (=Sampling Theorem, Shannon-Theorem) besagt, "daß ein bandbreitenbegrenztes Signal ohne Informationsverlust rekonstruiert werden kann, sofern die Abtastfrequenz mindestens doppelt so groß wie die maximale Signalfrequenz ist." (Zander, S. 705).
Enthält das abgetastete Signal Frequenzen, die über der halben Abtastfrequenz liegen, entstehen bei der AD-DA Umsetzung Frequenzen (Aliasfrequenzen, Spiegelfrequenzen), die im Originalsignal nicht enthalten waren. Um diesem als Aliasing bezeichneten Phänomen entgegenzuwirken, wird das Originalsignal vor der Abtastung durch einen Tiefpaßfilter in seiner Bandbreite begrenzt. Die Grenzfrequenz des Filters muß aufgrund begrenzter Flankensteilheit einen bestimmten Betrag unter der halben Abtastfrequenz liegen.
Da das wertkontinuierliche Analogsignal bei der Digitalisierung auf Werte einer endlichen Wertemenge abgebildet wird, kommt es zu Rundungsfehlern. Da diese Fehlerbeträge im Zeitverlauf statistisch verteilt auftreten, machen sie sich als Rauschen bemerkbar (Quantisierungsrauschen).
Um den tonalen Klangcharakter des Quantisierungsrauschens bei geringer Aussteuerung des abzutastenden Signals zu unterdrücken, wird dem Originalsignal vor der Digitalisierung eine geringe Rauschspannung (Dither-Rauschen) beigemischt. Auch bei der Requantisierung auf digitaler Ebene wird ein Dithersignal zugesetzt, um die dabei entstehenden Fehler zu maskieren.
Um die Dynamik des Originalsignals beizubehalten, muß der Signal/Rauschabstand der Dynamik des Originalsignals mindestens entsprechen. Die maximale Systemdynamik errechnet sich nach der Formel:
S/N [dB] = 6,02n + 1,76
Wobei n der Länge der Binärzahl in Bit entspricht.
Bei einer Auflösung von 16 Bit beträgt die maximale Systemdynamik demnach ca. 98 dB. Die tatsächlich nutzbare Dynamik und somit der effektive Signal/Rauschabstand liegt allerdings weit darunter, da ein bewerteter Störpegel von 14 dB, ein Schutzabstand zum Störpegel von 20 dB (Footroom) und eine Aussteuerungsreserve von 10 dB (Headroom) berücksichtigt werden müssen. Bei einer 16-Bit-Auflösung ergibt sich somit ein effektiver Signal/Rauschabstand von 54 dB.
D [dB] = 98 - 14 - 20 -10 = 54
Für Einsteiger:
Tafelbild zu Dezibel
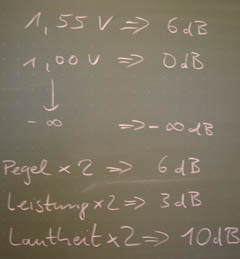
Verfahren digitaler Audiobearbeitung
62006 Großmann | WS 07/08
S | 1-4 | B2 | Di 14.15-15.45 | C 7.215 UC
Tutorium | Donnerstag 13.00 - 14.00 | 7.212 UC
Quelle: http://audio.uni-lueneburg.de/seminarwebseiten/sequenzing-neusite4.php, 05.03.2026